NCTM2017-Workshop Version

This is a post that contains links, files, and a general description for each of the activities I hope we get to.

NCTM2016 – Visualizing Mathematical Concepts

The 2016 NCTM Annual Meeting feels so far back now, but it was just last month.  I did a workshop on visualizing mathematical concepts to build connections.  I was honoured to have my session included in this great list.  And hence, rather than blog about my workshop here, please check out this page instead, or click on the image below.

TLAJ: Teach Like a Jedi – do NOT!

Being May the Fourth, my Twitter and Facebook are filled with Star Wars – which as a fan, I enjoy!  Then I saw a tweet with #tlap (Teach Like a Pirate) and thought, what about #tlaj: Teach Like a Jedi?

It didn’t take me long to see, wow, I kinda used to teach like that, and I’m glad I’m not the Jedi Master anymore.  Here are some quick thoughts on why I say “Teach Like a Jedi Do Not”:

• Jedi mind tricks: The very word tricks says it all! “You will FOIL this binomial product” “You will invert and multiply” “These aren’t the factors you’re looking for” “You will solve this problem this way” Let me do the mathematical thinking for you, and you just do what I do. That’s really what telling/showing is like for our learners. Sense-making and conceptual understanding are a hoped-for byproduct rather than a purposeful intention.
• “Do or do not, there is no try” Here’s how you do these questions, now do them. If you don’t get it, do it again and again until you do. Here, let me say it again, louder and slower.  No, I want my students to persevere in solving problems, to try and keep trying.
• The Force is strong in this one. Sure, there are strong math students, but every student can be successful in mathematics. Success is not limited just to the Padawans. My hope for future generations is that we never hear, “I was never good at math” again.
• In a similar vein, “I cannot teach him. The boy has no patience.” Ever heard those words before?

Some of these are more about being a Jedi or the beliefs of Jedi and not necessarily about how they teach, but I’m just having a bit of fun with it anyways. Feel free to share your own ideas in the comments.  There may also be worthwhile things to consider that are worth teaching like a Jedi, for example to trust your feelings/intuition.

Oh, and May the Fourth be with you!

Big Ideas in Patterning – Richmond Math Focus Day

I’ll add some more thoughts here later, but in the meantime, here are the documents from my workshop today.

Handout

Slides

NCTM2014 Workshop – I See It!

I was thrilled that so many showed up!  For those who were unable to make it (and for those who did and would like the files), here’s a run-through of what my session was about.  Sorry about the length of this post – I’m trying to re-live the workshop!  Here’s an overall outline in case you wish to jump to a particular section:

• Principles of Task Design
  • Pattern Exploration
  • Divisibility by 9
• Big Idea about Operations
  • Multiplication
  • Division
  • Division of Fractions
• Simplifying Radicals

First a few files.

• Here’s the handout that I provided for participants to play along for some of the activities.
• If you have Keynote, here are my slides. Note that this is for Keynote ’09. The newer version misses some of the table cell fills.
• Or here is a pdf version of the slides, sans animations of course.

I was honoured to have my session chosen for the Learn↔Reflect strand.  Here are the questions that were guiding the strand (with emphasis added):

1. What is number sense, and how can you promote the development of number sense in your students? How are fluency and understanding related in the context of number and operations?
2. How can instructional decisions facilitate the development of strategies that are meaningful and transferable for operations on all numbers?
3. How are equity and diversity promoted by developing conceptual understanding of number?
4. How can the Standards for Mathematical Practice support the development of number sense and computational fluency?
5. How are you thinking differently about your learning and teaching of number and operations as a result of participating in the Learn↔Reflect sessions?

My Principles of Task Design

I had some messages that I wanted to thread throughout my workshop, and I chose the umbrella of “principles” to do so.  As such, this is not an exhaustive list.

• Meaningful mathematics
  • Context or no – what matters most to me is that there be some real mathematics.
• Sense-making
  • This is my goal for my learners – this is what I think defines success, much more than getting right answers.  Does the math make sense?  And how? And what next?
• Who’s doing the math?
  • For years my reflective practice led to trying better and better ways to explain the math.  I made everything so clear, identified misconceptions and explained how to avoid them. Ummm… that wasn’t working.  It finally hit me, duh!, that I was the one doing the math – my students weren’t doing mathematics, they were just trying to do what I was doing.  Sense-making – not!
  • “I tell my students…” Oh, how many times I’ve heard that. Not that there aren’t some things which need to be told, but if sense-making is the goal, no amount of telling is going to do it, not for most learners anyways.
  • And what does it mean to do math? I like to think of math as a verb. Answer-getting, for its own sake, is not doing math.

Pattern Exploration

I’ve seen so many resources and online lessons which take a pattern-exploration approach to mathematical concepts.  This is a step in the right direction.  But I believe we can do better.  A future post will explore this further, but to give an example, let’s consider divisibility by 9.

Pattern approach:

• Examine numbers divisible by 9 (see slide for examples).
• Add up the digits.
• What do you notice?

Yep, this would hopefully lead to the conclusion of the rule for divisibility by 9.  But I think we can do better.  And while a nice symbolic proof makes us math people drool – such proofs may cause students to drool in a different way, ie. napping.

So consider this visual approach to divisibility by 9, with the specific example:
Is the number 387 divisible by 9?

Try making sense of this visually before reading below.

The Keynote slide shows a nice animation of one approach.  Here’s the end result:

One way of thinking of dividing by 9 is to make 9 groups.  If we take 1 away from each 100, what remains (99) can be divided into 9 groups.  Similarly so if we take 1 away from each 10. The overall divisibility by 9 is determined by whether the remaining number of 1s is divisible by 9 (ie. the red ones).  And this group is formed by 1 from each hundred, 1 from each ten, and the 1s – uh huh! – it’s the sum of the digits.  Extending this to larger numbers is not a difficult generalization to make.

A Big Idea about Number Operations

My colleague Chris Hunter developed an activity that we used for PD for our Secondary Mathematics Department Heads. It was framed around the following big idea:

The operations of addition, subtraction, multiplication, and division hold the same fundamental meaning 
no matter the domain to which they are applied. (Marian Small)

This is an idea that really came to life as I began to work in elementary classrooms. I encourage all secondary teachers that if you ever get a chance to spend some time thinking about, and even better, teaching elementary math, take it!  It will transform your secondary math classroom. I’m so grateful for all I’ve learned from my elementary colleagues!

Consider the operation of multiplication, specifically using an area model.  The same visualization and sense-making holds whether one be considering whole numbers, decimal numbers, or algebraic binomials (click on the image to view a more legible size):

Now for the next activity in the handout.  Evaluate, or simplify, each set of expressions.
Make as many connections as you can:

• conceptually & procedurally
• pictorially & symbolically

Take a moment and think of this before proceeding.

It is helpful when dividing to consider two different meanings of division (consider 6 ÷ 3):

• Partitive: Or sharing – If there are 3 groups, how many are in each group?
  
• Quotative: Or measurement – If there are groups of 3, how many groups? Or, how many 3s go into 6?
  

The numerical answers are the same, but the meaning and visualization are different.  Consider, which meaning helps make sense of (–6) ÷ (+3) ?
Which meaning makes sense of the fraction question?

Oh how crazy I was when I used to insist to students not to use a common denominator when dividing fractions, only use them for adding or subtracting.  A common denominator makes dividing fractions make more sense if we consider the quotative meaning!

I encourage you also to consider common numerator fraction division.  Then check out this from Christopher Danielson.

Next a quick example from Marian Small that I leave for you. Think in terms of the meaning of division.
Next consider this fraction question. A grid was provided if it helped.

Take some time.  How would you represent this division in a visual way?

Here’s one approach:
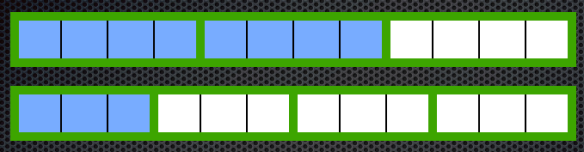One can make sense of the answers 2 2/3, or 8/3.  The key here is the common denominator (not that other approaches can not also make sense).  But don’t tell students that that’s what they need – they can be motivated to discover that need. First, they need to have in mind that the wholes for each fraction need to be the same. Then it’s about making sense of how we can reason to how many/much of the divisor goes into the dividend.

Here’s a TI-Nspire document that allows one to explore dividing fractions this way.  The fractions can be changed using sliders.

I highly encourage you to check out this post from Fawn Nguyen.

A couple of more things here.  One, there are other visualizations and representations (e.g.: I think cuisenaire rods and pattern blocks are fantastic) that work well here, and hence I didn’t require that one use the grid.  Second, this is the visual piece – I think it’s important to make symbolic connections as well.

Exploring Radicals

I didn’t have as much time as I’d like by this point of the workshop, but given radicals was in the title, we had to get to it!  This is also what I feel is the coolest part.  See the handout for the lesson.  I’ll give a brief summary.

What does square root mean visually?
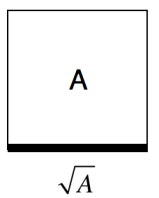I understood what square root means, but for so many years never thought to make the connection to its geometric meaning, but rather just relied on the numerical meaning when trying to teach about simplifying radicals.  Then one night (confession: I was enjoying a beverage with a colleague and what comes next was drawn on a napkin!), it occurred to me that there is a powerful connection between the geometric and numeric meanings of square root.  Consider a square whose area is 18.  Next consider how we may express the base of that square (ie. the square root) in different ways, visually! The key is to divide the large square into areas that we can express numerically, i.e. into squares, because we can use square roots to denote those lengths.

All of these bases are the same length.  Think about how to express them.

All of these are true equivalents, but one is the simplest, once we decide on what simplest means.  Also note, dividing into squares connects nicely to the numerical strategy of finding a square factor.  For more details, check out Chris Hunter’s blog post.

Technology-wise, I’ve created documents for both TI-Nspire and Geogebra. Click on the links to get the files.
That’s all folks!  One other idea I didn’t have time to get to was considering using graphs of log functions to determine logarithmic identities.

NCTM 2013 Denver – A Tweet Summary

I’m normally a prolific note-taker [Note: I’ll be posting about Evernote soon!], but I decided to take a different approach to my NCTM participation this year, and I’m glad I did!

Using Twitter proved to provide multiple benefits.  To name a few:

• More focused attention
  • I wasn’t distracted by writing constantly.
• Capturing the essence
  • The 140 character limit has intrinsic benefits.
• Participating on a global scale
  • Rather than stay isolated in my own notes, tweeting connected me with fellow attendees (sharing ideas & reflections – live!). It also opened the conversations up to those who weren’t able to attend that particular session,  as well as to those who weren’t at the conference.
• Broadening my Twitter-sphere
  • Many new followers and new people I followed – it’s a gift that keeps on giving!

So here are the tweets (mine and a selection of others via #NCTMDenver) for the sessions I attended (chronological order).  I’ve occasionally added a wee bit of commentary.  Admittedly, I should have taken a few pics along the way, and  I should have tweeted more.  Although nothing can replace being there, and these are but a few tidbits, I hope this offers something worthwhile. [Note: click on the images to view larger, more clearer, size].

2-The Power of Just One Teacher – Mayim Bialik (@missmayim)
Mayim Bialik, the Emmy-nominated actress on The Big Bang Theory and real-life neuroscientist, is on a mission to help educators and parents inspire students to pursue STEM education and careers. Bialik will share her nontraditional journey from child actress to neuroscientist to playing a scientist on TV and working with Texas Instruments.

Oops, slow start.  I actually didn’t tweet any thoughts on this one.  Overall, I did enjoy the session. Mayim was very genuine and engaging, especially during the Q&A. You can view her session here.  And here’s a sampling of others’ tweets:

Thanks to TI, I did get to attend a private reception with Mayim after:

And here’s the pic:

77-I See It: The Power of Visualization – yours truly
What does it mean to “see” the math? Taking concepts that are typically taught only symbolically, we’ll explore tasks that can engage students to reason and to make sense of mathematical concepts through visual representations. The nature of these tasks will include concrete patterning, dynamic graphing, geometric representation, and more.

I’ll post about my session separately.  In the meantime, here’s my handout.

184-Keeping It Real: Teaching Math through Real-World Topics – Karim Kai Ani (@karimkai and @Mathalicious)
How long does burning off a Big Mac take? In basketball, should you ever foul at the buzzer? Explore real-world lessons that teachers can immediately use to address the Common Core State Standards in a fresh, new way. Learn to foster a rigorous understanding of math while challenging students to think about the world more critically.

246-Technology in Support of Proof – Tom Dick
Technology can provide a “conjecture generator,” where we use its power to find mathematical patterns that might lead to the formulation of a conjecture. Proving such a conjecture is often viewed outside the use of technology. We will examine several examples where technology offers powerful hints to mathematical structure that aid in proof.

Caveat: the number of tweets is not necessarily a measure of the quality of a session. For this one I just watched and enjoyed – I’ve long been a fan of Tom’s purposeful and meaningful use of technology.  The highlight was using a TI-Nspire spreadsheet to explore the limit of the ratio of consecutive terms of the Fibonacci sequence (no matter what the first two terms are, even if they’re complex!).

NCTM Trivia / Happy Hour
Come get your beer & trivia on with @desmos, with special guests @mathalicious, and emcee @ddmeyer

Not in the program, but what a great time! We had the whole bar to ourselves and it was packed.  Dan did a fabulous job emceeing.  Best category of trivia: functions expressed through sound! (courtesy of Desmos – an unreleased but very cool feature)

Team π-fection, by the way, was myself, Dona McSpadden, Chris Becker (@ChrisBecker67), and Benjamin Graber (@MathExplorers).

354-Essential Mindsets for Tilling the Soil for the Common Core – Steven Leinwand (@steve_leinwand)
With the game-changing nature of the Common Core State Standards, leadership from all of us is a nonnegotiable element to shepherd and support their implementation. This session will answer the questions, “How should we be positioning ourselves?” and “What must we be doing?” so that we do not squander this once-in-a-lifetime opportunity.

POWERFUL session, and Twitter reflected this.  So, here’s a long but not exhaustive list:

411-Keeping Our Eyes on the Prize – Philip Uri Treisman
NCTM has committed itself to equity, with many of us working toward a new generation of mathematics-savvy citizens and STEM professionals representing our diverse population. We need to take stock of the record and take action from the state house to the classroom, so that our vision becomes reality and our hopes for our students are realized.

I wasn’t at this session, but seeing the Twitter feed made me wish that I had been.  You can view his session here.

483 – Take Time to Question the Questions – Mark Howell
With the help of technology, math teachers have a rich array of engaging exploration environments to lay before students. It takes thoughtful reflection, though, to construct meaningful and appropriate questions. We will see activities from algebra, geometry, and calculus and explore what makes a question good.

534 – Creating Opportunities for Students to Engage in Reasoning and Proof – Margaret (Peg) Smith
Although there is a growing consensus that the grades 7–12 curriculum needs greater emphasis on reasoning and proof, research shows that most textbooks offer limited opportunities to engage in these practices. We will focus on how to modify tasks to give students more opportunities to engage in reasoning and proving.

560 – Powerful Online Tools Promote Powerful Mathematics – Eli Luberoff (@desmos) and Patrick Vennebush
The free calculator available from Desmos (www.desmos.com) allows for exceptional graphing. Combine this tool with the resources at Illuminations (http://illuminations.nctm.org) to create powerful lessons. Learn how to combine these two resources to craft exceptional mathematical experiences for your students. BYOD, and get ready to get funky.

634 – They’ll Need It for Calculus – Christopher Danielson (@Trianglemancsd)
What ideas do middle school students need for calculus? Maybe not what you think. They need an awareness of change, approximation, and accumulation. We will work middle school tasks that use these ideas, and we will consider how these ideas build into the major ideas of calculus.

An early morning start, but a great crowd showed up. Go here to see Christopher’s blog post about his session.

684 – Tools and Technology for Modern Math Teaching – Dan Meyer (@ddmeyer)
A lot of new tools and technology exist to help our students learn more meaningful mathematics. The question you may have now is, “Which tools deserve our limited time and resources?” I will offer a framework to guide you toward useful tools and more modern math teaching.

Always a must-see, always inspiring, always powerful, always witty, always… you get the idea.

724 – Viral Math Videos: A Hart-to-Hart Conversation – Vi Hart (@vihartvihart) and George Hart
Father and daughter, George and Vi Hart make videos in their own styles with the common goal of showing real, awesome, beautiful math. Vi learned some math from George, and George learned about videos from Vi, and you can learn how they create content that educates, inspires, and makes people want to share.

And that concludes my NCTM 2013 experience, and I’d have to say it was the best NCTM conference I’ve been to (I think this was my 6th).  To the many speakers whose sessions I wanted to go to but could not make it to, I hope to see you next year – #NCTMNewOrleans!

———————————————————

Note: I owe a lot of gratitude to my great friend, Dona McSpadden, who lent me her mifi throughout the conference. The wifi seemed to disappear strangely when going into a meeting room, but I was able to be connected always.  It came in handy for a couple of presenters as well!

Pop Goes the Weasel – NOT!

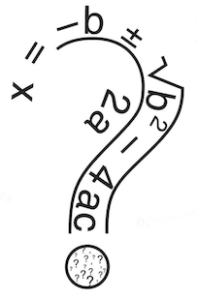
I love the quadratic formula – what self-respecting math geek wouldn’t? I would always wear my best suit on the day of the quadratic formula lesson. Somehow, my students didn’t seem to share in the joy the same way I did. Adding a “Pop Goes the Weasel” song raised the joy-level a wee bit, but my goal of mathematical joy was nowhere to be seen.

One of the lessons I shared at my “Different Approaches to Familiar Topics” workshop aims to change that – if not more joyous, at least let’s make solving quadratic equations using a formula more meaningful.

Getting Started

Here’s the student handout (QuadraticEquations). It begins with activating prior knowledge – solving a quadratic equation by graphing, and algebraically (non-formula). More importantly, there is a connection between the graphical and algebraic solutions.

Here’s the equation, with an algebraic solution:

Wait a minute, why the box around the penultimate step, instead of the answer?  Because the answer doesn’t tell the whole story, the box step says so much more. Consider the graphical solution:

See the connection? Don’t tell students the connection – they will find it (hence the question prompt in the handout).  Yes, the zeros are symmetric about the axis of symmetry – obvious to us math geeks, but why should we have all the fun?

Generalizing

On to page 2.  It’s time to generalize.  Once again, don’t do this for the students – they can do it themselves; and then they can do the sense-making.

Alrighty then, a new formula, but one that makes sense.  A prompt for students, and for you: Explain and illustrate the meaning of this formula in terms of the graph of a quadratic function.

Let’s not underestimate the power of connections. The formula connects symbolic meaning to graphical meaning.  Sure, there’s some meaning with the traditional formula, but how many make sense of the axis of symmetry being  , let alone the meaning of  ?

The Discriminant

Consider the –k/a. How much more meaningful is this than b² – 4ac? Real solutions require that k and a be opposite – a fact that has obvious graphical meaning, as does the situation that makes for equal solutions.

Page 3

The third page of the handout just gives three equations to solve. Two of them are not in vertex form. That doesn’t disqualify them from this formula. Converting these to vertex form in a meaningful way – that’s for a future blog post. It’s also cause to think about what kinds of equations we ask students to solve.  In contextual problems, modeling often makes much more sense using vertex form – perhaps this form should be predominant for quadratic equations.

Pop Goes the Weasel – NOT

We don’t need a song for this formula. I think it just makes sense.

———————————————————————-

Entering the Land of Make Believe

This isn’t part of the handout, but an idea for an extension. That negative sign inside the radical is begging to be noticed. Consider the equation (x – 3)² + 4 = 0. Using the formula we get x = 3 ± 2i. The symmetry is there, of course, but what about graphical meaning? Let’s give that negative sign some i-dentification.

Graphically, what is the meaning of this radicand compared to the previous? It’s opposite – graphically we can represent this by making a opposite or k opposite. And presto! The complex roots now have graphical meaning:

Making ‘a’ opposite reveals the complex roots.

Oh, there’s also a way to get graphical meaning to cubic functions that have complex roots.  That too may be the subject of a future post, perhaps when I’m feeling super geeky. In the meantime, why not try it yourself?

One More Thing

Another piece that isn’t on the handout – actually I just thought of it. Ever try to come up with quadratic functions or equations that have rational roots? Playing around with different values for a, b, and c to make b² – 4ac a perfect square isn’t fun. Yes, there are other ways (factored form, etc.), but just note how easy it is to make –k/a a perfect square. Indeed we can quite directly consider a whole family of quadratic functions that have rational roots.  Let’s make another connection – a visual representation. Consider the function y = (x + 3)² – 4, which has integral roots given -k/a = 4.  Modeling this with algebra tiles:

And these tiles rearrange nicely into a completed rectangle.

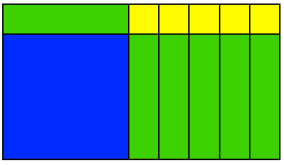Coincidence? No! Connection? Yes! A quadratic function with rational roots is always factorable.  Think of this in reverse too – more connections to be made. In particular, think of how the factors relate to the value of h.

This would also be cool to visualize using colour tiles, a la this blog from Chris Hunter.

Different Approaches to Familiar Topics

It was an honour and a privilege to present today to such a great group of passionate mathematics teachers at the Northwest Mathematics Conference in Victoria, BC.  With apologies again for those who did not get a handout, you can click on the image below to download a pdf of it.

Click here to download a pdf of my handout.

I’ll make a point of posting a blog about at least two of these activities in the near future.

Welcome to my blog

My first blog is coming, but in the meantime you can check out my About page.